
BitNetのternary量子化がSIMDと相性抜群な理由
「CPUだけで60,000 tokens/sec」
この数字を見て、最初は信じられませんでした。GPUなしで、どうやってそんな速度が出るのか?
答えはBitNetのternary量子化とSIMDの組み合わせにありました。この記事では、なぜこの組み合わせが「相性抜群」なのかを、図解を交えて解説します。
1. 通常のLLM推論が遅い理由
ニューラルネットワークの基本演算
LLMの推論で最も時間がかかるのは行列積です。
output = weight × input
weight: 重み行列(モデルのパラメータ)
input: 入力ベクトル(トークンの埋め込み)
浮動小数点演算のコスト
通常のLLMは32bit浮動小数点(FP32)や16bit浮動小数点(FP16)を使用します。
weight: 0.12345678 (32bit float)
input: 0.87654321 (32bit float)
↓
output: 0.12345678 × 0.87654321
= 0.10821...(浮動小数点乗算)
浮動小数点乗算は重い処理です:
- 指数部と仮数部の計算
- 正規化処理
- 丸め処理
これらが大量に発生するため、計算コストが高くなります。
2. BitNet 1.58bitの革新
重みを3値に制限
BitNet 1.58bitは、重みを {-1, 0, +1} の3値のみに量子化します。
通常のLLM:
weight ∈ [-∞, +∞] (連続値)
BitNet 1.58bit:
weight ∈ {-1, 0, +1} (3値のみ)
なぜ「1.58bit」?
3値を表現するのに必要なビット数:
log₂(3) = 1.585...bit ≈ 1.58bit
実装上は2bitで格納(00=-1, 01=0, 10=+1)
乗算が不要になる魔法
ここが最大のポイントです。重みが3値しかないため、乗算が不要になります。
weight = -1 の場合:
-1 × x = -x
→ 符号ビットを反転するだけ!乗算不要
weight = 0 の場合:
0 × x = 0
→ 計算自体をスキップ!
weight = +1 の場合:
+1 × x = x
→ そのまま使う!乗算不要
結論: 浮動小数点乗算が整数の加減算に置き換わります。
3. SIMDとは
Single Instruction, Multiple Data
SIMDは「1命令で複数のデータを同時処理」する技術です。
通常の処理(スカラー):
a[0] + b[0] → c[0] (1回目)
a[1] + b[1] → c[1] (2回目)
a[2] + b[2] → c[2] (3回目)
a[3] + b[3] → c[3] (4回目)
→ 4命令必要
SIMD処理(ベクトル):
a[0:3] + b[0:3] → c[0:3] (1回で4つ同時)
→ 1命令で完了!
主なSIMD命令セット
| 命令セット | ビット幅 | 同時処理数(8bit整数) | プラットフォーム |
|---|---|---|---|
| SSE | 128bit | 16個 | x86 (古め) |
| AVX2 | 256bit | 32個 | x86 (主流) |
| AVX-512 | 512bit | 64個 | x86 (最新) |
| NEON | 128bit | 16個 | ARM |
| SVE | 可変 | 可変 | ARM (最新) |
4. BitNet + SIMDの相性が良い理由
理由1: 演算が単純
BitNetの演算:
result = Σ (weight[i] × activation[i])
weight[i] ∈ {-1, 0, +1} なので:
= Σ (-activation[i] または 0 または +activation[i])
= 加算と減算のみ!
整数の加減算はSIMDで最も高速な演算の1つです。
理由2: データが小さい
通常のLLM:
weight: 32bit float × N個
→ 128bit SIMDレジスタに 4個 しか入らない
BitNet:
weight: 2bit × N個
→ 128bit SIMDレジスタに 64個 入る!
同じレジスタで16倍のデータを処理可能です。これにより、メモリ帯域の節約にも繋がります。
理由3: 分岐が不要
// 分岐あり(遅い)
for (int i = 0; i < N; i++) {
if (weight[i] == -1) result -= activation[i];
else if (weight[i] == 1) result += activation[i];
// weight == 0 は何もしない
}
// SIMDで分岐なし(速い)
// マスク演算で一括処理
neg_mask = (weights == -1); // どれが-1か
pos_mask = (weights == +1); // どれが+1か
result = sum(activations & pos_mask) - sum(activations & neg_mask);
SIMDを使うことで、if文の分岐予測ミスによるペナルティをゼロにできます。
5. 具体的な数値で見る高速化
1トークンあたりの演算量
LLaMA 7Bモデルの場合:
通常(FP16):
パラメータ: 7B × 16bit = 14GB
演算: 7B × 浮動小数点乗算
BitNet 1.58bit:
パラメータ: 7B × 2bit = 1.75GB(1/8)
演算: 7B × 整数加減算
実測値(Bit-TTT)
| 指標 | 数値 |
|---|---|
| 推論速度 | 60,000 tokens/sec |
| 使用CPU | 一般的なデスクトップCPU |
| GPU | 不使用 |
速度の内訳
- メモリ帯域: 1/8のデータ量 → 8倍高速
- 演算速度: 整数演算 → 10倍以上高速
- SIMD効率: 16倍のデータ並列 → 16倍高速
- キャッシュ効率: データが小さい → ヒット率向上
これらが組み合わさり、数十〜数百倍の高速化が実現されています。
6. 実装のポイント
AVX2での実装例(疑似コード)
// 256bit AVX2レジスタで32個の8bit整数を同時処理
__m256i process_bitnet(
__m256i activations, // 32個の8bit活性化値
__m256i weights // 32個の2bit重み(パック済み)
) {
// 重みを展開
__m256i neg_mask = _mm256_cmpeq_epi8(weights, neg_one);
__m256i pos_mask = _mm256_cmpeq_epi8(weights, pos_one);
// 条件付き加減算
__m256i neg_vals = _mm256_and_si256(activations, neg_mask);
__m256i pos_vals = _mm256_and_si256(activations, pos_mask);
// 集約
return _mm256_sub_epi8(pos_vals, neg_vals);
}
Rustでの実装
Candleフレームワークは内部でSIMD最適化を行っています。
use candle::{Device, Tensor};
// Candleが自動でSIMD最適化
let result = weights.matmul(&activations)?;
明示的なSIMDコードを書かなくても、ライブラリが最適化してくれるため、開発者はロジックに集中できます。
7. 図解:全体の流れ
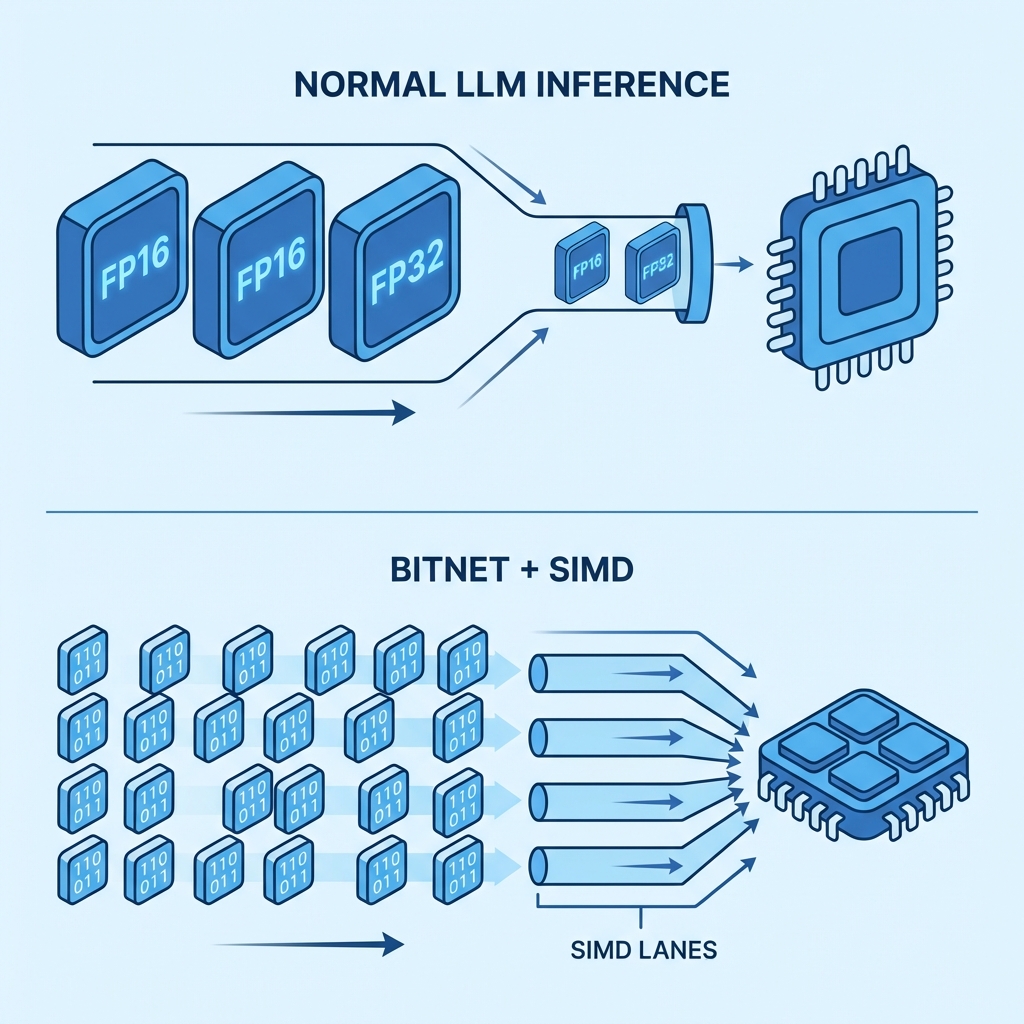
通常のLLM推論では、FP32/FP16の巨大なデータをGPUに転送し、多くの電力を消費して計算します。一方、BitNet + SIMDでは、コンパクトなデータをCPUのSIMDレーンに詰め込み、超並列で一気に処理します。これが「CPUだけで爆速」のからくりです。
8. 注意点と制約
精度への影響 & メリット・デメリット
メリット:
- 推論速度: 数十〜数百倍
- メモリ使用量: 1/8〜1/16
- 消費電力: 大幅削減
デメリット:
- 精度低下: あり(ただし実用上は許容範囲内)
- 学習: 特殊な手法が必要(QAT等)
- モデル互換性: 専用の変換が必要
向いているユースケース
- エッジデバイス(スマホ、IoT)
- 大量リクエストの処理
- リアルタイム応答が必要な場面
- 電力制約がある環境
まとめ
| 技術 | 役割 |
|---|---|
| BitNet 1.58bit | 重みを{-1,0,+1}に量子化し、演算を単純化 |
| SIMD | 多数のデータを1命令で同時処理 |
| 組み合わせ | CPUで60,000 tokens/secを実現 |
「単純な演算」×「大量並列」= 爆速
これがBitNet + SIMDの相性が良い理由です。低レイテンシが求められるアプリケーションや、ローカルLLMの活用において、この技術は重要な役割を果たしていくでしょう。
参考リンク
- BitNet: Scaling 1-bit Transformers (論文)
- Bit-TTT実装(Qiita)
- Intel Intrinsics Guide
- ARM NEON Programmer's Guide
※この記事はYui AIプロジェクトでの技術検討をもとに作成しました